
This site documents the Divine Mind:
the Universe that enables us to create ourselves
page 20: space-time—the cosmic memory and operating system
Table of contents
20.1: The power of evolution lies in variation, selection and memory
20.2: Physics and theology in a divine universe
20.3: Impasse—gravity, relativity and quantum field theory
20.4: Another approach—from von Neumann's kinematic formalism to dynamic reality
20.5: Cantor's digitization of continuity and the transfinite numbers
20.6: Gravitation, codeless communication, built in memory and local individuation
20.7: Photons are eternal
20.1: The power of evolution lies in variation, selection and memory
In scientific investigations . . . it is permitted to invent any hypothesis, and if it explains various large and independent classes of facts, it rises to the rank of a well grounded theory. Charles Darwin (1875): The variation of animals and plants under domestication
We begin with the initial singularity, an eternal empty set, the permanent foundation of the Universe. A key step in any project to establish that the Universe is divine is the unification of theology, which deals with the spiritual dimension of human existence, and physics, which deals with our material situation. Traditional theology has often dismissed this problem by holding that the material world is just a transitory phase in our existence. When the end comes the material world will be transformed into something completely consistent with the human spirit. Here this view is barely relevant since theology as we have it is not even a science, but simply a restatement of ancient mythology interpreted by organizations like the Roman Catholic Church as divine revelation. Theology, as it currently exists, must be completely rebuilt on physical, biological, psychological and political evidence to become a real science.
Mathematically we may think of naked gravitation as an omnipotent empty set. Now that it has developed Hilbert space, quantum mechanics, particles, fermions and bosons and Minkowski space it is ready for the next steps. The first step is to develop the global structure described by Einstein's general relativity, and the second to populate itself with more particles of different varieties within the general classification of bosons and fermions. As quantum evolution increases number and variety of elementary particles with different communication protocols, it becomes more probable that they will bind into more complex networks which may eventually come alive and be able to reproduce themselves and evolve according to the standard protocols of biological evolution.
Darwin’s theory is the simplest and most powerful scientific theory ever developed. It is in effect the much sought after theory of everything, the theory of creation. He used it to explain the origin of species in the vast and complex tree of life. The theory explains how hundreds of millions of species descended over billions of years from a primordial life form. This initial species was a biological analogue of the initial singularity. All life on Earth appears to be related through descent from this common source. It may not have been the first life form on our planet, but it is the one that survived to become the root of our current tree of life. This fact is shown by the similarity of all forms of life at the level of molecular biology. Last universal common ancestor - Wikipedia, Tree of life (biology) - Wikipedia, Molecular biology - Wikipedia
Here we are hoping to use the process of evolution to describe the origin of the Universe from a structureless initial singularity. This singularity is formally identical to the Christian God described by Aquinas, eternal, omnipotent and the creator of the Universe. This does not seem to be a lot to go on but it may be all we need. Aquinas, Summa, I, 3, 7: Is God altogether simple?
We now have detailed understanding the evolutionary process in the context of life. How can we extend it back to the moment when the Universe was a structureless initial singularity? How can this minimal system implement the three features of the evolutionary paradigm, variation, selection and memory?
Every living creature carries two copies of itself. One is its actual physical self; the other is an abstract formal representation of itself encoded in its genes. The genes serve as abstract messengers between generations. Working through the molecular mechanisms in a fertilized egg, they control the development of the new individual and account for the fact that species breed true. Variations in the genes arise from mutations, transcription errors and the superpositions of genes from two parents. The circumstances of life also account for some individual differences in the children.
On the whole the rate of genetic change is slow so that, as Darwin realized, it can take millions of years and millions of generations of incremental change for to develop a new species. Once developed some species remain relatively unchanged for tens of millions of years. The ultimate control of survival rests in the selective process. Some individuals survive and reproduce. Many, often most, do not. Although biological reproduction is a well defined process, there are many ways for it to fail, particularly because almost all living things are subject to predation by other living creatures. There is nothing like the divine guidance postulated by the old theologies and religions. Generally species, once they have become adapted to their environment, only change if their environment changes. We still know very little about the detailed origin of life and genetics.
Evolution is a slow and meticulous process with a very long memory. Life began about 4 billion years ago, and billions of species have appeared and disappeared since then. The slow process of variation and selection enables it to pay meticulous attention to detail down to the atomic and molecular level, working in the context of both quantum and classical mechanics. As we learn the details of the molecular foundations of life that have become visible since the invention of electron microscopes, xray diffraction and other technologies we see that every element of living bodies has been carefully shaped to create the complex dynamic mechanisms of life. Evolutionary history of life - Wikipedia, William Bialek & Allan Schweitzer (1985): Quantum noise and the threshold of hearing
The stability of the genetic memory enables evolution to build on its past successes. The variation between generations enables life to explore new possibilities. We can extrapolate evolution back to the initial singularity because we can trace its essential elements, variation, selection and memory back to the beginning. A remarkable feature of this history appears to be that the first particles to emerge into space-time, the massless bosons, play the role of genes, carrying quantum states unchanged along null geodesics through space and time. We may imagine the Universe as a "tree of particles" bound together by bosons that play a role similar to genes, communicating information between generations of particles.
Massless bosons serve as memory because they travel at the speed of light on null geodesics in Minkowski space. This means that the are effectively outside space and time, eternal as long as they exist. Their moment of creation is identical to their moment of annihilation even if they travel billions of light years in between. Earth is bathed in the cosmic microwave background which was formed about 14 billion years ago, only a few hundred thousand years after the Universe began to emerge within the initial singularity. Cosmic microwave background - Wikipedia
The previous pages on this site have proposed a simple mechanism for this development exploiting the model of divinity that has emerged since ancient people began to search for an evidence based picture of the world. They have not always been on the right track. We need a paradigm change to provide a contemporary understanding of the relationships between spirit, matter, knowledge, and reality.
Nevertheless there does not seem to be any evolution among fundamental particles. As far as we can tell the sixty or so we have now are identical to those that appeared the beginning. We find, in high energy accelerator experiments that no matter what we do the same zoo of particles appears spontaneously or they may evolve almost instantaneously. The elementary particles unite in various ways to form atoms. The variety of atoms is also quite limited. There are about 100 different elements, appearing as nearly 300 isotopes with the same electronic arrangements but different nuclei. Elementary particle - Wikipedia, Isotope - Wikipedia
The variety of available structures explodes when we come to molecules. The simplest, like oxygen and hydrogen appear as two identical atoms. Water comprises two atoms of hydrogen and one oxygen. Carbon dioxide, one carbon and two oxygen. Large organic molecules may contain hundred or thousands of atoms. A protein like haemoglobin in blood comprises about 10 000 atoms of hydrogen, carbon, nitrogen, oxygen and sulfur and four atoms of iron which form the oxygen binding site.
The old paradigm, referred to frequently in previous pages, considers the creator to be an omniscient and omnipotent immaterial being. This being created the world according to a pre-existing plan. The task of science seen as the study the Universe as we find it to elucidate this plan. The evolution of science has recorded many remarkable and far reaching changes in our understanding of our world. In general these changes have led to increases in equality, welfare, reproductive success and population. Evolution has provided us with a generic paradigm to follow the overall development of the world. The most recent major development in physics is quantum field theory whose first major success was the story of light and matter which began in the 1860's with Kirchoff's study of black body radiation. Thomas Piketty (2022): A brief history of equality, Black-body radiation - Wikipedia, Richard Feynman (1988): QED: the strange story of light and matter
20.2: Physics and theology in a divine Universe
My project to unite physics with theology in a divine universe is well supported by the deep relationships between physics, logic, philosophy and mathematics which date back 2500 years to the ancient Greeks Plato, Aristotle and their contemporaries. This relationship was renewed by Galileo in the seventeenth century by his observation of the central role of mathematics in physics:
Philosophy is written in this grand book - the universe, which stands continually open before our gaze. But the book cannot be understood unless one first learns to comprehend the language and to read the alphabet in which it is composed. It is written in the language of mathematics . . .. Galileo Galilei (1610, 1957) : Discoveries and opinions of Galileo: including the Starry Messenger, p 238.
Newton reinforced this view with his mathematical model of the solar system. The relationship between mathematics and physics became slightly problematic with Hilbert's introduction of formalism at the beginning of the twentieth century. Although most mathematicians are at home with concepts like infinity, transfinity, real numbers and continuity, it is often difficult to decide whether a mathematical concept really represents physical reality. Here I feel that a lot of trouble springs from the idea that the background or canvas of quantum mechanics is continuous spacetime.
From an engineering point of view, physics has steadily transformed human existence from earliest times. Much of our way of life is built on significant physical contributions to building and construction, defence, water supply and agriculture. All the modern developments in transport, energy production, transport, communication and computation have deep physical roots. The defining constraints in international political relationships (defined by Clausewitz's statement: War is merely the continuation of policy by other means) are built around nuclear weapons and the technologies for their construction and delivery. These and almost all other technologies are intimately related to quantum mechanics and quantum field theory, the leading edge of modern physical research and development.
The physics industry is very proud of the standard model based on quantum field theory. Modern physics began when Galileo and his contemporaries questioned the work Aristotle which had been the standard model of the world for nearly two thousand years. Aristotle's ideas had been embraced by the medieval Catholic Church and given quasi dogmatic status. Galileo and the astronomers Copernicus, Brahe and Kepler took their lives in their hands when they dared to suggest that the Church was on the wrong track. Reality triumphed in the world of Newton. He avoided lethal criticism by casting his work as an explanation of the magnificence of divine creation. Galileo affair - Wikipedia, Isaac Newton (1713): The general scholium to the Principia Mathematica
Newton's model of the solar system was based on his law of universal gravitation. He assumed that massive bodies were attracted to one another by a force that varied as the product of their masses divided by the square of the distance between them. He saw this force as part of God's design and could not say how it worked. Newton's law of universal gravitation - Wikipedia
Newton's work founded classical physics, the study of massive slow moving objects like planets and motor vehicles. He also observed the spectrum of white light and realized that there must be other forces in the world yet to be observed and described. The future of physics was revealed when at the beginning of the nineteenth century Alessandro Volta invented a chemical battery which could supply continuous electric currents. This enabled the experimental study of the relationship between magnetism and electric current. Sixty years later James Maxwell devised a set of equations which showed that light is an electromagnetic phenomenon, a harmonic oscillator cycling between electric current and magnetism. Alessandro Volta - Wikipedia, Maxwell's equations - Wikipedia
Michael Faraday, a skilled experimenter, introduced field as an influence filling space that accounted for the forces exerted by electric currents and magnets. He showed how to visualize magnetic fields with iron filings. Many saw the field idea as overcoming the mystery of action at a distance that faced Newton. The idea of a continuous fields coupled with discrete quanta is now central to quantum field theory, the heart of modern physics. Michael Faraday - Wikipedia
In 1859 Gustav Kirchoff set physics toward quantum mechanics with his law of thermal radiation:
For a body of any arbitrary material emitting and absorbing thermal electromagnetic radiation at every wavelength in thermodynamic equilibrium, the ratio of its emissive power to its dimensionless coefficient of absorption is equal to a universal function only of radiative wavelength and temperature. That universal function describes the perfect black-body emissive power. Kirchoff's law of thermal radiation - Wikipedia
In 1901 Max Planck ended the search for Kirchoff's universal function with his law of distribution of energy in the normal spectrum based on the idea that radiation was emitted in discrete packets or quanta. Quantum mechanics was born. Planck's law - Wikipedia
In 1905 Einstein proposed that Planck's quanta were in fact the real particles which we now call photons. At that time the wave nature of light was very firmly entrenched and it took the Nobel Prize people took a long time to award Einstein for his work. When he finally got to speak he lectured about relativity, not the photoelectric effect. Albert Einstein (1905c): On a heuristic point of view concerning the production and transformation of light, Albert Einstein (1923): Nobel Lecture: Fundamental ideas and problems of the theory of relativity
In 1924 Louis de Broglie proposed that the wavelike nature of fundamental particles like the electron could be used to describe the stationary eigenfunctions in their interactions. This inspired Schrödinger's wave equation and his understanding of quantum theory as an eigenvalue problem. This led to von Neuman's development of abstract Hilbert space as a mathematical foundation for the theory. Louis de Broglie (1929): Nobel lecture: the wave nature of the electron, Erwin Schrödinger (1926): Quantization is an eigenvalue problem, John von Neumann (2014): Mathematical foundations of quantum mechanics
The quantum mechanics of discrete particles came of age in the late 1920's. The state of an isolated particle is represented by the unitary evolution of state vectors in Hilbert space governed by the Schrödinger equation:
where H is the energy (or Hamiltonian) operator.
In Hilbert space, where there is no space, time or energy the variable t and the operator H are elements of a mathematical formalism that is not necessarily connected to time and energy.
Our knowledge of quantum theory comes from measurement which involves interaction of particles. I discuss some aspects of quantum interaction on page 14: Measurement—the interface between the Minkowski and Hilbert spaces. The key idea is that when two particles interact the state vectors associated with them are treated as a linear combination in the tensor product of the Hilbert spaces associated with each particle.
20.3: Impasse—relativity, gravity and quantum field theory
The picture of mechanics described so far operates in Newtonian space, a combination of Euclidean space and conventional universal time, completely independent of space and motion in space.
Einstein began his paper on special relativity by stating a contemporary electrodynamic problem:
It is well known that Maxwell's electrodynamics—as usually understood at present—when applied to moving bodies, leads to asymmetries that do not seem to attach to the phenomena. [. . .]. Albert Einstein (1905): On the electrodynamics of moving bodies
He solved this problem, not by modifying electrodynamics, but by uniting space and time in a new entity, spacetime. Einstein's work sent a slow shock wave through physics which eventually had a significant impact on quantum mechanics. Its implication for classical dynamics was made explicit by Hermann Minkowski in his Address to the 80th Assembly of German Natural Scientists and Physicians, (September 21, 1908):
The views of space and time which I wish to lay before you have sprung from the soil of experimental physics, and therein lies their strength. They are radical. Henceforth, space by itself, and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality.'Minkowski space - Wikipedia, Hermann Minkowski (1908): Space and Time – lecture given at the 80th Meeting of the Natural Scientists in Cologne.
It soon became clear that quantum theory must embrace special relativity. The question was: How?
For a while people like Bohr thought that this had been achieved by Klein and Gordon with the Klein-Gordon equation, a modification of the Schrödinger equation to embrace the quadratic relativistic relationships of mass, time and momentum. Klein-Gordon equation - WikipediaDirac, on the other hand, thought that time should be linear, and that energy should be linearized to match the time. He also started with the Schrödinger equation but sought to take the square root of the energy rather than to square the time:
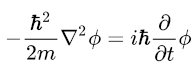
Explaining the origin of quantum field theory Weinberg writes:
The point of view of this book is that quantum field theory is the way it is because (with certain qualifications) this is the only way to reconcile quantum mechanics wth special relativity. Therefore our first task is to study how symmetries like Lorentz invariance appear in a quantum setting. Steven Weinberg (1995): The quantum theory of fields: volume I
From the point of view of the science of physics, the radical problem with field theory is that although it provides very complex (but computably executable) descriptions of three domains of particle physics: electrodynamics, the weak interaction and the strong integration, it appears to be facing insurmountable difficulties when it comes to gravitation.
The problem seems to lie in renormalization. This technique has been developed to remove unwanted unphysical infinities in the theory. From my point of view renormalization is unecessary because it is an answer to a mathematically imposed problem that started with the proof, based on the Pythagorean theorem, that spacetime is continuous. Anthony Zee, discussing a seventeenth century problem that troubled Newton, writes:
A location for hell had to be found. Every epoch in physics has its own top ten problems. It is conceivable that future generations would find our desperate attempts to quantize gravity absurd. Anthony Zee (2018): On Gravity: a brief tour of a weighty subject, page 22, Renormalization - Wikipedia
Quantum field theory is a child of classical field theory. The leading achievement in classical field theory is Einstein's general theory of relativity which he built on the special theory of relativity which he published in 1905. In the conclusion to his paper on the field equations of gravitation he wrote:
In two recently published papers I have shown how to obtain field equations of gravitation that comply with the postulate of general relativity, i.e., which in their general formulation are covariant under arbitrary substitutions of space-time variables. . . . With this, we have finally completed the general theory of relativity as a logical structure. The postulate of relativity in its most general formulation (which makes space-time coordinates into physically meaningless parameters) leads with compelling necessity to a very specific theory of gravitation that also explains the movement of the perihelion of Mercury. However, the postulate of general relativity cannot reveal to us anything new and different about the essence of the various processes in nature than what the special theory of relativity taught us already.Albert Einstein (1915): The Field Equations of Gravitation
20.4: Another approach—from von Neumann's kinematic formalism to dynamic reality
Since general relativity is built on special relativity, we might expect the answer to the quantization of Einstein gravitation to lie in the nature of Minkowski space.
My effort to unite theology and physics has led me to modifications in both disciplines. Theology requires a complete revision to convert it from literary fiction to science. Physics also has a number of difficulties which appear in quantum field theory associated with the appearance of the confusion noted by Kuhlman.
Kuhlmann writes:
In conclusion one has to recall that one reason why the ontological interpretation of QFT is so difficult is the fact that it is exceptionally unclear which parts of the formalism should be taken to represent anything physical in the first place. And it looks as if that problem will persist for quite some time. Meinard Kuhlmann (Stanford Encyclopedia of Philosophy): Quantum Field Theory
Further problems arise from the appearance of unphysical infinities that must be removed by renormalization, first mentioned on page 5: God's ideas, cybernetics and singularity
The story proposed here is a hybrid union of traditional theology and a variant interpretation of modern physics. This union is built on the assumption that the Universe is divine, which implies that physics and theology must be consistent with one another. My story takes the form of an account of the evolution of the Universe within an initial singularity formally identical to the traditional Christian model of God.
I feel that an answer to the difficulties implicit in a field theory that treats spacetime as a mathematical continuum is to reverse the order of Minkowski and Hilbert space, making Hilbert space the foundation of the Universe and deriving Minkowski space from Hilbert space. The idea is to treat gravitation as the source of the energy that endows the forms of particles created by quantum mechanics with concrete reality. This is outlined on page 17: Gravitation and quantum theory—in the beginning.
From a modern point of view we can see quantum mechanics as a language which serves both for communication and for computation. Shannon's theory shows that computation is an intrinsic element of coding and decoding communications. We (and the Universe) spend much of our effort trying to work out how to say things and to understand what is being said. The mathematical theories of communication and computation suggest that quantum mechanics is capable of saying anything sayable, including the structure of Minkowski space which appears to be built on the fact that all the fundamental particles we observe in the world fall into one of two categories, boson or fermion. Nielsen & Chuang (2016): Quantum Computation and Quantum Information, John S. Bell (1987): Speakable and Unspeakable in Quantum Mechanics
We understand the distinction between fermions and bosons to be based on a rather mysterious property we call spin. In the cognitive layer of the world I understand the quantum of action to be a logical operator. It appears in real Minkowski space with the dimensions of angular momentum, hence the name spin. Concrete particles with integral spin are bosons and have a tendency to flock together. Particles with odd half integral spin like electrons and the other particles and antiparticles described by the Dirac equation obey the Pauli exclusion principle and refuse to occupy identical quantum states. This means that in real spacetime fermions cannot occupy the same point. This property is understood to explain the electronic structure of atoms and to account at a fundamental level for the spatial extension of all material structures.
The distinction between fermions and bosons may be explained by a difficult piece of mathematics known as the spin statistics theorem. This theorem may be understood as a consequence of special relativity or, alternatively, special relativity and Minkowski space and may be consequences of quantum theory. Papers like Duck and Sudarshan, not to mention most of quantum theory, are beyond my comprehension. Can we prove the spin-statistics theorem or the statistics-spin theorem? It is not really necessary if it is an observable product of evolution. Can we prove the existence of a rabbit? We can observe their existence, but any proof would have to connect the terabytes of data that go into an actual rabbit to a suitable set of axioms. The only set we have are implicit in evolution. Ian Duck and E.C.G. Sudarshan (1998): Toward an understanding of the spin-statistics theorem
Let us therefore proceed on the basis that the guess I made on page 12: The quantum creation of Minkowski space is correct. Evidence for this view is the fact that Minkowski space is considered to be pixellated by the quantum of action according to the relationship ΔE.Δt ≈ Δp.Δx ≈ ℏ.
The Nyquist-Shannon theorem shows that we can digitize continuous signals, and suggests the existence of algorithms to recover the continuous original from the digital representation. This idea explains the peculiar metric of Minkowski space. It provides null geodesics for the massless bosons and a solid 3D space which enables fermions to avoid each other, like air traffic in space. Nyquist-Shannon sampling theorem - Wikipedia
The passage from Minkowski space to general relativity passes through Riemann's differential geometry. Although this mathematical theory is expressed in terms of calculus and real numbers the combination of the weakness of gravitation and the smallness of the quantum of action suggests that there would be little to be gained from a computational point of view if we possessed a quantum theory of gravitation. Differential geometry - Wikipedia, Albert Einstein & Marcel Grossman (1913): Outline of a Generalized Theory of Relativity and of a Theory of Gravitation
The emergence of the Universe within the initial singularity is in effect the creation of a memory containing the algorithms that define the behaviour of the world. This information is located in both elementary particles and larger particles, like atoms, ourselves, planets and stars, constructed from elementary particles. The first 19 pages of this site contain some ideas about how this might happen. The whole process, as I see it, is derived from the fact that the initial singularity is a topological space that meets the requirements of fixed point theory as described on page 9: The active creation of Hilbert space.
One way to look at the list of troubles cited in Kuhlman's article is that they all arise from misapplications of mathematics which have been built in during the history of the subject.
Kuhlmann explains that QFT is an extension of quantum mechanics (QM) dealing with particles to fields, that is to continuous systems with an infinite number of degrees of freedom. QFT arose from partially successful reconciliation of QM and special relativity theory (SRT). The infinities that arose from the application of continuous mathematics to a quantized universe were dealt with by renormalization. Kerson Huang (2013): A critical history of renormalization
An outstanding example of the the problems arising in quantum field theory is the problem discussed at length on page 18.7: The cosmological constant problem. Here the infinite formal or kinematic states of the system are considered to be real, concrete and dynamic, giving a computational result in error by a factor of approximately 10100.
This appears to be a consequence of a more fundamental problem which arises from the assumption derived from classical theory that Minkowski space is the domain of Hilbert space. Here the delocalization of quantum theory and the reality of entanglement are taken to show that Hilbert space is in fact completely independent of Minkowski space and is not affected by the special theory of relativity: see page 13: Is Hilbert space independent of Minkowski space?
Physics, as we know it, studies the present condition of the Universe in the hope of understanding how it works. It has arrived, in the last century or so, at the fairly comprehensive theory of the three species of fundamental forces, electromagnetism, the weak force and the strong force. Pais records much of this story. At present progress has come to a halt because there seems to be no way to extend quantum field theory to include gravitation. Pais (1986): Inward Bound: of matter and forces in the physical world20.5: Cantor's digitization of continuity and the transfinite numbers
The ancient discovery of the Pythagorean theorem led to the idea that there may be real numbers between the rational numbers. This and the representation of functions using Fourier series led Georg Cantor to the idea of "derived sets". His idea was that as well as there being real numbers between the rational numbers, there may further numbers between the real numbers and so on ad infinitum. He then turned this idea around. Looking at this idea in terms of numbers of "points" rather than their "size" led him to the concept of transfinite numbers. He began with the smallest infinite set, the countably infinite set of rational numbers. He coined the new symbol aleph zero, ℵ0 to represent the cardinal of this set. The cardinal of the set of real numbers between the rational numbers became ℵ1, and he imagined an unending sequence ℵ2, ℵ3, . . . of transfinite cardinals. Georg Cantor (1897, 1955): contributions to the founding of the theory of transfinite numbers, Joseph Dauben (1990): Georg Cantor: His Mathematics and Philosophy of the Infinite
Cantor thought seriously about theology and felt that his mathematical ideas had a theological application. This upset some theologians who thought only God could be infinite, and it also introduced problems like Cantor's Paradox into mathematics since if Cantor's theorem was valid there could be no greatest cardinal number to represent God. Cantor's paradox - Wikipedia
Nineteenth century mathematics, particularly Cantor's invention of the transfinite numbers, threw up other problematic logical paradoxes. A major attempt to deal with this problem is Whitehead and Russell's Principia Mathematica, based on the idea that the paradoxes are consequences of the ambiguity of natural language. They proposed that mathematics could be cleaned up by expressing it in well defined symbolic language without natural nuances. Hilbert proposed a similar idea, formalism, cutting mathematics off from physical analogies and treating it as a purely symbolic game. The players could invent any symbols, define them by any axioms and manipulate them with trustworthy logical functions provided only that their results did not lead to contradiction. Whitehead and Russell (1910): Principia Mathematica, Hilbert's program - Wikipedia
Hilbert's program endows mathematicians with the same powers and limitations as we have attributed to the divine initial singularity on this site. It is omnipotent, and can therefore do anything consistent. It is ignorant and so, like a formalist starting from scratch, there are no initial constraints on its behaviour. Insofar as mathematics is a creative cognitive enterprise, we might also understand the Hilbert method of mathematics as the key to the process through which the Universe creates itself: cognitive cosmogenesis. It is not just a user of mathematics; it is maker of mathematics. We might ask where is the arithmetic in a bag of beans?. Cantor answered this by creating one to one correspondences between beans and the elements of sets. Using sets, he created arithmetic. Michael Hallett (1984): Cantorian set theory and limitation of size On page 9: The active creation of Hilbert space we imagine how the initial singularity, acting as a mathematical mind, might create the abstract Hilbert space developed for quantum mechanics by John von Neumann. The keys to the process are fixed point theory and Turing computable functions. Page 17: Gravitation and quantum theory—in the beginning describes how the singularity might use the kinematics of quantum theory and the energy available from gravitational potential to create the real dynamic spacetime and the particles within it that constitute the Universe. We imagine that each new particle created in the universe is analogous to the initial singularity, a real dynamic entity associated with a Hilbert space which acts in effect as its mind and controls its interactions with other particles in the Universe. Like the persons of the Trinity that began my story, each new particle may have children of its own. The Trinity is limited to three persons by ancient dogma. Here we recognize no such limit. Life and death, the creation and annihilation of particles, are parts of the universal process: (see page 8: The theology of the Trinity).We imagine this Hilbert space to be in kinematic perpetual motion driven by the power of the dynamic initial singularity. Although this entity may exist before the emergence of spacetime it is already subject to a simple constraint analogous to the ancient idea that every angel is a unique species. Up until the last few centuries people believed that matter is the principle of individuation. Since angels are immaterial it was concluded that they could only be differentiated by being formally different. In mathematical language, we would say that angels are orthogonal. Since Hilbert space exists outside spacetime, emergence of a basis state identical to one already existing would add nothing to the complexity of the space, just as two identical angels would be just one angel unless they are distinguished by something outside themselves like space. This idea is reflected in the no cloning theorem of quantum theory. Principle of individuation - Wikipedia, Aquinas, Summa I, 50, 4: Is every angel a different species?, No cloning theorem - Wikipedia
Another feature of Hilbert space, which it has in common with all mathematical statements is that it is formal, abstract or kinematic, like Plato's forms. Aristotle invented the unmoved mover to move the Platonic forms because he knew they could not move themselves. Similarly, mathematics does not do itself. It must be done by some dynamic entity capable of moving itself and formal kinematic objects like Hilbert spaces. Theory of Forms - Wikipedia, Unmoved mover - Wikipedia, Aristotle: Metaphysics: Book xii, vi, 2: The role of the unmoved mover
20.6: Gravitation, codeless communication, built in memory and local individuation
On page 17: Gravitation and quantum theory—in the beginning we described how the formal kinematic process of quantum mechanics identified stationary points which then derived energy from the the bifurcation of gravitation into potential and kinetic energy to become real particles with kinetic energy. This process was devised as a replacement for the quantum field theoretical idea that abstract fields are realized as concrete particles by deriving energy from the vacuum whose energy content arises rather mysteriously from the uncertainty principle thought to be implicit in the the finite quantum of action. (see Page 18.7: The cosmological constant problem.)
Gravitation is an exceedingly weak force and we can observe the relationship between gravitational potential and kinetic energy as they are embodied in the action of a pendulum. It is clear that the potential energy of a pendulum in its high position is exactly equivalent to its kinetic energy in the low position but this kinetic energy is almost negligible compared to the actual relativistic energy of the pendulum mass m, so this idea that concrete particles derive their energy from gravitational potential does appear a little far fetched. Nevertheless we will stand by the idea that the application of energy to make abstract particles concrete introduced on page 17 is consistent with the idea explained on page 16: Potential + kinetic = zero energy universe as it applies to the Universe as a whole, rather than to some local pendulum. It avoids the difficulty that seems to be implicit in the big bang theory that all energy in the Universe is already present in the initial singularity.
Richard Feynman set a multitude of ideas loose into the world of physics. Two of these are in the background to this site, quantum computation and quantum gravitation. We start with quantum gravity and spin 2 gravitons. Structures are built by communication and the more complex structures require more complex communication, which is why this site is such an undigested mess. The complexity of communication, as Claude Shannon taught us, is measured by entropy. Because gravitation is 4D, Feynman may assume that the graviton must have spin 2 in order to have sufficient entropy to define spacetime. Richard Feynman (2002): Feynman Lectures on Gravitation
If ever quantum gravitation is proved true this may be the case, but here we have fantasized about constructing Minkowski space with spin 1 particles, bosons which flock together, are massless and can carry unlimited amounts of energy, and spin ½ fermions which obey the Pauli exclusion principle, avoid one another and need three dimensions for free movement. Now we want to take our little pieces of flat Minkowski space into a Universe and we are working under two principal constraints. Whatever we (and the fledgling Universe) do must be consistent, and it must be simple because the initial singularity within which we are working is absolutely simple like the Christian God. It is omnipotent and its only guidance is that it is impossible for it to do anything impossible. This means that, like Hilbert's formalist mathematics and Cantor' transfinite numbers, it is logically confined. To go outside it is to go nowhere.
We made our little 4D Minkowski spaces with spin ½ and spin 1 particles whose form, we assume, is accessible to quantum mechanics and whose concrete reality is built, on the basis of a zero energy Universe, by the bifurcation of naked gravitation into potential (negative) and kinetic (positive) energy which add up to zero. Negative energy is hard to understand. On the basis of the fundamental formula of quantum mechanics E = hf, it implies that time goes backwards. From a second law of thermodynamics point of view, we do not like to see complex structures disassembling themselves, but we see no problem in a system like the initial singularity which has no structure.
From a mathematical point of view, Einstein gravitation describes a closed Universe. This is in effect circular and so curved in spacetime. Like a black hole, assumed to be structureless, we cannot get out of it. This closure appears as curvature and explains the applicability of the mathematical mechanism of differential geometry.
Our next hurdle is the angel problem. Cantor's theorem is a formal constructive proof for the existence of transfinite numbers based on the idea that a set of n objects (cardinal n) may be split into n2 subsets and n2 is always greater than n as long as n is an integer greater than 1 and the property holds when n is countably infinite. We assume that the hierarchy of transfinite numbers goes on forever. This works formally, but how does it work if the elements we consider are real and concrete? To make the mathematics work, they must be created and differentiated.
Quantum field theory divides the fundamental forces, that is communication links, into four classes. Electrodynamics uses massless photons, chromodynamics uses massless gluons, the weak interaction uses the massive W and Z spin 1 bosons, and the massive Higgs particle, spin 0. Gravitation couples to every particle that has energy, that is every real or concrete particles and so we might call it codeless communication. Communication theory shows us how network communications may be differentiated by the code or language used. From this point of view gravitation and quantum theory speak to everybody.
Because they are so simple, they both share the possibility of reversibility which is built into quantum mechanics by unitarity. This guarantees that all the speech uttered in the Universe between its participants is normalized. This feature was used by von Neumann to demonstrate the identity of matrix and wave mechanics.
Now to Plato, forms and angels and Plato's nemesis Aristotle. From Plato's point of view there is only one Form of the Good, which some might have identified with God when Judaism and Christianity assimilated Platonism. In reality there are many goods, and the Aristotelian medieval scholastics assumed that matter was the principle that distinguished them: it is the principle of individuation. In order to make Cantor's theorem work and populate the Universe with a vast number of elementary particles, and ourselves made from these particles, we need individuation.
The modern equivalent of matter is energy, m = E/c2 but it seems that energy itself does not differentiate. What differentiates is the form of energy and the creator of form is quantum mechanics as discussed on page 19.2: Quantum mechanics is a language. Plato reduced the number of forms to one for each property of the world. Aristotle, on the other hand, multiplied them by attaching them to matter. Now we can create infinities of different forms using the mechanisms described by Cantor, aided by quantum evolution made possible by the intelligent linearity built into quantum mechanics and the endless energy available from the omnipotent initial singularity, divine naked gravitation. All concrete forms are instances of memory. We first designed a computer separating memory from process. The cognitive Universe, like our own brains, contains memory and process in a single concrete structure.
Like the variation and selection in biological evolution, there are stable possibilities hidden in the variety of kinematic quantum activity which are selected for survival by the mathematical operators of quantum mechanics described in page 10: the emergence of quantum mechanics.
20.7: Photons are eternal
We assume that the first real particles to come into existence in the universe are photons of random energy. Let us understand a photon be the transformation of a pure kinetic hilbert basis state into a physical particle by receiving energy from the gravitational potential. While a photon exists in Minkowski space between its creation and its annihilation it is an eternal element of real dynamic memory, implementing the priciple that information is physical. Because it is massless and travelling at the speed of light it follows a null geodesic, carrying a quantum state from the source which created it to the destination where the state is passed on and the photon annihilated. From the point of view of an observer time is stopped on a photon, it is non-existent. The quantum phase of the photon does not advance. Kevin Brown (2018): Reflections on relativity, page 693
The photon is a perfect memory, reading the data supplied when it was formed and writing it when it is annihilated. The photons of the cosmic background are about 14 billion years old. their energy has been reduced by climbing the gravitational gradient from near the big bang, but their phase is unchanged since no time has elapsed in their frame.
Simple particles like photons do not have internal degrees of freedom which can be changed like more complex particles such as hadrons and atoms. In order carry a message they must be created and annihilated. When the electron in an atom or molecule interacts with a photon its energy and its state within the atom is changed, and we may understand this as the annihilation of one state and the creation of another whose parameters are determined by the phase and energy of the photon and the electron's state within the atom.
(revised Friday 3 January 2025)
copyright:
you may copy this material freely provided only that you quote fairly and provide a link (or reference) to your source.
notes and references
Further reading
Books
Adams (1999), Marilyn McCord, Horrendous Evils and the Goodness of God, Melbourne University Press 1999 Jacket: 'Thinkers in all societies have struggled to make sense of horrendous evil. This provocative book takes a religious perspective. It tackles a fundamental dilemma in Christian thought -- how to reconcile faith in God with the evils that afflict human beings.
Distinguished American philosopher Marilyn McCord Adams argues that analytic philosophy of religion is too narrowly focussed. The ground rules for debate have allowed philosophers to avert their gaze from the very worst evils and from their impact on human lives.
She proposes a radical shift away from the preoccupation with morals and towards more fruitful evaluative categories such as purity, defilement, honour, shame and aesthetics. The innovative approach of Horrendous Evils and the Goodness of God will challenge thinkers both religious and secular.'
|
Augustine (419, 1991), and Edmond Hill (Introduction, translation and notes), and John E Rotelle (editor), The Trinity, New City Press 399-419, 1991 Written 399 - 419: De Trinitate is a radical restatement, defence and development of the Christian doctrine of the Trinity. Augustine's book has served as a foundation for most subsequent work, particularly that of Thomas Aquinas.
|
Bell (1987), John S, Speakable and Unspeakable in Quantum Mechanics, Cambridge University Press 1987 Jacket: JB ... is particularly famous for his discovery of a crucial difference between the predictions of conventional quantum mechanics and the implications of local causality . . . . This work has played a major role in the development of our current understanding of the profound nature of quantum concepts and of the fundamental limitations they impose on the applicability of classical ideas of space, time and locality.
|
Brown (2018), Kevin, Reflections on Relativity, 2018 ' . . . general relativity teaches us that the principles of special relativity are applicable only over infinitesimal regions in the presence of gravitation, so in a sense the general theory restricts rather than generalizes the special theory. However, we can also regard special relativity as a theory of flat four-dimensional spacetime, characterized by the Minkowski metric (in suitable coordinates), and the general theory generalizes this by allowing the spacetime manifold to be curved, as represented by a wider class of metric tensors. It is remarkable that this generalization, which is so simple and natural from the geometrical standpoint, leads almost uniquely to a viable theory of gravitation.' (page 700)
|
Cantor (1897, 1955), Georg, Contributions to the Founding of the Theory of Transfinite Numbers (Translated, with Introduction and Notes by Philip E B Jourdain), Dover 1895, 1897, 1955 Jacket: 'One of the greatest mathematical classics of all time, this work established a new field of mathematics which was to be of incalculable importance in topology, number theory, analysis, theory of functions, etc, as well as the entire field of modern logic.'
|
Darwin (1859, 2001), Charles, and Ernst Mayr, On the Origin of Species: A Facsimile of the First Edition, Harvard University Press 2001 Amazon review: 'It was a very happy idea to publish a facsimile of the first edition of On the Origin of Species; the price of copies of the original edition has reached the thousand dollar bracket, and in contemporary literature all page-references are to the original pagination, which was not followed in previous reprints of the first edition. Now, with this very reasonably priced and beautifully produced book, not only historians of science but also biologists will have the opportunity of following the fascinating thought-trails, still far from fully explored, of that remarkable man Darwin. Few if any persons are so well qualified as Harvard's Ernst Mayr to execute so helpfully and gracefully the delicate task of writing a worthy foreword to such a classic.'
--Sir Gavin de Beer (Science )
|
Darwin (1859), Charles, The Origin of Species: By Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life, Cambridge University Press 1859, 2009 ' It's hard to talk about The Origin of Species without making statements that seem overwrought and fulsome. But it's true: this is indeed one of the most important and influential books ever written, and it is one of the very few groundbreaking works of science that is truly readable. . . .
Darwin's friend and "bulldog" T.H. Huxley said upon reading the Origin, "How extremely stupid of me not to have thought of that." Alfred Russel Wallace had thought of the same theory of evolution Darwin did, but it was Darwin who gathered the mass of supporting evidence—on domestic animals and plants, on variability, on sexual selection, on dispersal—that swept most scientists before it.' Mary Ellen Curtin
|
Darwin (1875), Charles, and Harriet Ritvo (Introduction), The Variation of Animals and Plants Under Domestication (Foundations of Natural History), Johns Hopkins University Press 1875, 1998 ' "The Variation, with its thousands of hard-won observations of the facts of variation in domesticated species, is a frustrating, but worthwhile read, for it reveals the Darwin we rarely see -- the embattled Darwin, struggling to keep his project on the road. Sometimes he seems on the verge of being overwhelmed by the problems he is dealing with, but then a curious fact of natural history will engage him (the webbing between water gun-dogs' toes, the absurdly short beak of the pouter pigeon) and his determination to make sense of it rekindles. As he disarmingly declares, 'the whole subject of inheritance is wonderful.'.
|
Dauben (1990), Joseph Warren, Georg Cantor: His Mathematics and Philosophy of the Infinite, Princeton University Press 1990 Jacket: 'One of the greatest revolutions in mathematics occurred when Georg Cantor (1843-1918) promulgated his theory of transfinite sets. . . . Set theory has been widely adopted in mathematics and philosophy, but the controversy surrounding it at the turn of the century remains of great interest. Cantor's own faith in his theory was partly theological. His religious beliefs led him to expect paradox in any concept of the infinite, and he always retained his belief in the utter veracity of transfinite set theory. Later in his life, he was troubled by attacks of severe depression. Dauben shows that these played an integral part in his understanding and defense of set theory.'
|
Dirac (1983), P A M, The Principles of Quantum Mechanics (4th ed), Oxford UP/Clarendon 1983 Jacket: '[this] is the standard work in the fundamental principles of quantum mechanics, indispensible both to the advanced student and the mature research worker, who will always find it a fresh source of knowledge and stimulation.' (Nature)
|
Feynman (1988), Richard, QED: The Strange Story of Light and Matter, Princeton UP 1988 Jacket: 'Quantum electrodynamics - or QED for short - is the 'strange theory' that explains how light and electrons interact. Thanks to Richard Feynmann and his colleagues, it is also one of the rare parts of physics that is known for sure, a theory that has stood the test of time. . . . In this beautifully lucid set of lectures he provides a definitive introduction to QED.'
|
Feynman (2002), Richard, Feynman Lectures on Gravitation, Westview Press 2002 ' The Feynman Lectures on Gravitation are based on notes prepared during a course on gravitational physics that Richard Feynman taught at Caltech during the 1962-63 academic year. For several years prior to these lectures, Feynman thought long and hard about the fundamental problems in gravitational physics, yet he published very little. These lectures represent a useful record of his viewpoints and some of his insights into gravity and its application to cosmology, superstars, wormholes, and gravitational waves at that particular time. The lectures also contain a number of fascinating digressions and asides on the foundations of physics and other issues. '
|
Hallett (1984), Michael, Cantorian Set Theory and Limitation of Size, Oxford UP 1984 Jacket: 'This book will be of use to a wide audience, from beginning students of set theory (who can gain from it a sense of how the subject reached its present form), to mathematical set theorists (who will find an expert guide to the early literature), and for anyone concerned with the philosophy of mathematics (who will be interested by the extensive and perceptive discussion of the set concept).' Daniel Isaacson.
|
Hawking (1975), Steven W, and G F R Ellis, The Large Scale Structure of Space-Time, Cambridge UP 1975 Preface: Einstein's General Theory of Relativity . . . leads to two remarkable predictions about the universe: first that the final fate of massive stars is to collapse behind an event horizon to form a 'black hole' which will contain a singularity; and secondly that there is a singularity in our past which constitutes, in some sense, a beginning to our universe. Our discussion is principally aimed at developing these two results.'
|
Hopkins (2001), Keith, A World Full of Gods: The Strange Triumph of Christianity, Penguin Random House 2001 ' In this provocative, irresistibly entertaining book, Keith Hopkins takes readers back in time to explore the roots of Christianity in ancient Rome. Combining exacting scholarship with dazzling invention, Hopkins challenges our perceptions about religion, the historical Jesus, and the way history is written. He puts us in touch with what he calls “empathetic wonder”—imagining what Romans, pagans, Jews, and Christians thought, felt, experienced, and believed-by employing a series of engaging literary devices. These include a TV drama about the Dead Sea Scrolls; the first-person testimony of a pair of time-travelers to Pompeii; a meditation on Jesus’ apocryphal twin brother; and an unusual letter on God, demons, and angels.'
|
Lonergan (2007), Bernard J F, and Michael G Shields (translator), Robert M Doran & H Daniel Monsour (editors), The Triune God: Systematics (Collected Works, volume 12), University of Toronto press 2007 De Deo trino, or The Triune God, is the third great instalment on one particular strand in trinitarian theology, namely, the tradition that appeals to a psychological analogy for understanding trinitarian processions and relations.
The analogy dates back to St Augustine but was significantly developed by St Thomas Aquinas. Lonergan advances it to a new level of sophistication by rooting it in his own highly nuanced cognitional theory and in his early position on decision and love. . . . This is truly one of the great masterpieces in the history of systematic theology, perhaps even the greatest of all time.'
|
Nielsen (2016), Michael A., and Isaac L Chuang, Quantum Computation and Quantum Information, Cambridge University Press 2016 Review: A rigorous, comprehensive text on quantum information is timely. The study of quantum information and computation represents a particularly direct route to understanding quantum mechanics. Unlike the traditional route to quantum mechanics via Schroedinger's equation and the hydrogen atom, the study of quantum information requires no calculus, merely a knowledge of complex numbers and matrix multiplication. In addition, quantum information processing gives direct access to the traditionally advanced topics of measurement of quantum systems and decoherence.' Seth Lloyd, Department of Quantum Mechanical Engineering, MIT, Nature 6876: vol 416 page 19, 7 March 2002.
|
Pais (1986), Abraham, Inward Bound: Of Matter and Forces in the Physical World, Clarendon Press, Oxford University Press 1986 Preface: 'I will attempt to describe what has been discovered and understood about the constituents of matter, the laws to which they are subject and the forces that act on them [in the period 1895-1983]. . . . I will attempt to convey that these have been times of progress and stagnation, of order and chaos, of belief and incredulity, of the conventional and the bizarre; also of revolutionaries and conservatives, of science by individuals and by consortia, of little gadgets and big machines, and of modest funds and big moneys.' AP
|
Pais (1991), Abraham, Niels Bohr's Times, in Physics, Philosophy and Polity, Clarendon Press 1991 Jacket: 'The life of Niels Bohr spanned times of revolutionary change in science itself as well as in its impact upon society. Along with Albert Einstein, Bohr can be considered to be this century's major driving force behind the new philosophical and mathematical descriptions of the structure of the atom and the nucleus.
Abraham Pais, the acclaimed biographer of Albert Einstein, here traces Bohr's progress from his well-to-do origins in late nineteenth-century Denmark to his position at centre stage in the world political scene, particularly during the Second World War and the development of atomic weapons.'
|
Piketty (2022), Thomas, A Brief History of Equality, Harvard UP 2022 ' The world's leading economist of inequality presents a short but sweeping and surprisingly optimistic history of human progress toward equality despite crises, disasters, and backsliding. A perfect introduction to the ideas developed in his monumental earlier books.It's easy to be pessimistic about inequality. We know it has increased dramatically in many parts of the world over the past two generations.'
|
Weinberg (1995), Steven, The Quantum Theory of Fields Volume I: Foundations, Cambridge University Press 1995 Jacket: 'After a brief historical outline, the book begins anew with the principles about which we are most certain, relativity and quantum mechanics, and then the properties of particles that follow from these principles. Quantum field theory then emerges from this as a natural consequence. The classic calculations of quantum electrodynamics are presented in a thoroughly modern way, showing the use of path integrals and dimensional regularization. The account of renormalization theory reflects the changes in our view of quantum field theory since the advent of effective field theories. The book's scope extends beyond quantum elelctrodynamics to elementary partricle physics and nuclear physics. It contains much original material, and is peppered with examples and insights drawn from the author's experience as a leader of elementary particle research. Problems are included at the end of each chapter. '
|
Zee (2018), Anthony, On Gravity: a brief tour of a weighty subject, Princeton UP 2018 Jacket: ' Inspired by Einstein's audacious suggestion that somehow spacetime could ripple, Zee begins with the stunning discovery of gravity waves. He foes on to explain how gravity can be understood in comparison to other classical field theories, presents the idea of curved spacetime and the action principle, and explores cutting edge topics including black holes and Hawking radiation. Zee travels as far as the theory reaches, leaving us with tantalizing hints of the utterly unknown, from the intransigence of quantum gravity to the mysteries of dark matter and energy.'
|
Links
Albert Einstein (1905), On the Electrodynamics of Moving Bodies, ' It is well known that Maxwell's electrodynamics-as usually understood at present—when applied to moving bodies, leads to asymmetries that do not seem to attach to the phenomena. Let us recall, for example, the electro-dynamic interaction between a magnet and a conductor. The observable phenomenon depends here only on the relative motion of conductor and magnet, while according to the customary conception the two cases, in which, respectively, either the one or the other of the two bodies is the one in motion, are to be strictly differentiated from each other. For if the magnet is in motion and the conductor is at rest, there arises in the surroundings of the magnet an electric field endowed with a certain energy value that produces a current in the places where parts of the conductor are located. But if the magnet is at rest and the conductor is in motion, no electric field arises in the surroundings of the magnet, while in the conductor an electromotive force will arise, to which in itself there does not correspond any energy, but which, provided that the relative motion in the two cases considered is the same, gives rise to electrical currents that have the same magnitude and the same course as those produced by the electric forces in the first-mentioned case.' back |
Albert Einstein (1905c), On a heuristic point of view concerning the production and transformation of light, ' The wave theory of light, which operates with continuous spatial functions, has proved itself splendidly in describing purely optical phenomena and will probably never be replaced by another theory. One should keep in mind, however, that optical observations apply to time averages and not to momentary values, and it is conceivable that despite the complete confirmation of the theories of diffraction, reflection, refraction, dispersion, etc., by experiment, the theory of light, which operates with continuous spatial functions, may lead to contradictions with experience when it is applied to the phenomena of production and transformation of light. Indeed, it seems to me that the observations regarding "black-body" light, and other groups of phenomena associated with the production or conversion of light can be understood better if one assumes that the energy of light is discontinuously distributed in space.' back |
Albert Einstein (1915), The Field Equations of Gravitation, ' In two recently published papers I have shown how to obtain field equations of gravitation that comply with the postulate of general relativity, i.e., which in their general formulation are covariant under arbitrary substitutions of space-time variables. . . . With this, we have finally completed the general theory of relativity as a logical structure. The postulate of relativity in its most general formulation (which makes space-time coordinates into physically meaningless parameters) leads with compelling necessity to a very specific theory of gravitation that also explains the movement of the perihelion of Mercury. However, the postulate of general relativity cannot reveal to us anything new and different about the essence of the various processes in nature than what the special theory of relativity taught us already.' back |
Albert Einstein (1923), Nobel Lecture: Fundamental ideas and problems
of the theory of relativity, ' The conclusion is obvious that any arbitrarily moved frame of reference is equivalent to any other for the formulation of the laws of Nature, that there are thus no physically preferred states of motion at all in respect of regions of finite extension (general relativity principle). |
Albert Einstein & Marcel Grossman (1913), Outline of a Generalized Theory of Relativity and of a Theory of Gravitation, ' The theory expounded in what follows derives from the conviction that the proportionality between the inertial and the gravitational mass of bodies is an exactly valid law of nature that must already find expression in the very foundation of theoretical physics. I already sought to give expression to this conviction in several earlier papers by seeking to reduce the gravitational mass to the inertial mass; this endeavor led me to the hypothesis that, from a physical point of view, an (infinitesimally extended, homogeneous) gravitational field can be completely replaced by a state of acceleration of the reference system. This hypothesis can be expressed pictorially in the following way: An observer enclosed in a box can in no way decide whether the box is at rest in a static gravitational field, or whether it is in accelerated motion, maintained by forces acting on the box, in a space that is free of gravitational fields (equivalence hypothesis).' back |
Alessandro Volta - Wikipedia, Alessandro Volta - Wikipedia, the free encyclopedia, 'Alessandro Giuseppe Antonio Anastasio Volta (18 February 1745 – 5 March 1827) was an Italian physicist and chemist who was a pioneer of electricity and power who is credited as the inventor of the electric battery and the discoverer of methane. He invented the voltaic pile in 1799, and reported the results of his experiments in 1800 in a two-part letter to the president of the Royal Society.' back |
Antiparticle - Wikipedia, Antiparticle - Wikipedia, the free ecyclopdia, ' In particle physics, every type of particle of "ordinary" matter (as opposed to antimatter) is associated with an antiparticle with the same mass but with opposite physical charges (such as electric charge). For example, the antiparticle of the electron is the positron (also known as an antielectron). While the electron has a negative electric charge, the positron has a positive electric charge, and is produced naturally in certain types of radioactive decay. The opposite is also true: the antiparticle of the positron is the electron.' back |
Aquinas, Summa I, 25, 3, Is God omnipotent?, '. . . God is called omnipotent because He can do all things that are possible absolutely; which is the second way of saying a thing is possible. For a thing is said to be possible or impossible absolutely, according to the relation in which the very terms stand to one another, possible if the predicate is not incompatible with the subject, as that Socrates sits; and absolutely impossible when the predicate is altogether incompatible with the subject, as, for instance, that a man is a donkey.' back |
Aquinas, Summa I, 50, 4, Is every angel a different species?, ' . . . such things as agree in species but differ in number, agree in form, but are distinguished materially. If, therefore, the angels be not composed of matter and form, as was said above (Article 2), it follows that it is impossible for two angels to be of one species; just as it would be impossible for there to be several whitenesses apart, or several humanities, since whitenesses are not several, except in so far as they are in several substances.' back |
Aquinas, Summa, I, 3, 7, Is God altogether simple?, 'I answer that, The absolute simplicity of God may be shown in many ways. First, from the previous articles of this question. For there is neither composition of quantitative parts in God, since He is not a body; nor composition of matter and form; nor does His nature differ from His "suppositum"; nor His essence from His existence; neither is there in Him composition of genus and difference, nor of subject and accident. Therefore, it is clear that God is nowise composite, but is altogether simple. . . . ' back |
Aristotle 1071b12, Metaphysics book XII, vi, 2: The role of the unmoved mover, ' But even if we are to suppose that there is something which is kinetic and productive, although it does not actually move or produce, there will not necessarily be motion; for that which has potentiality may not actualise it. Thus it will not help matters if we posit eternal substances, as do the exponents of the Forms, unless there is in them some principle which can cause change. . . . therefore there must be a principle of this kind whose essence is actuality.' back |
Black-body radiation - Wikipedia, Black-body radiation - Wikipedia, the free encyclopedia, 'Black-body radiation is the type of electromagnetic radiation within or surrounding a body in thermodynamic equilibrium with its environment, or emitted by a black body (an opaque and non-reflective body) held at constant, uniform temperature. The radiation has a specific spectrum and intensity that depends only on the temperature of the body.' back |
Born rule - Wikipedia, Born rule - Wikipedia, the free encyclopedia, ' The Born rule (also called the Born law, Born's rule, or Born's law) is a law of quantum mechanics which gives the probability that a measurement on a quantum system will yield a given result. It is named after its originator, the physicist Max Born. The Born rule is one of the key principles of the Copenhagen interpretation of quantum mechanics. There have been many attempts to derive the Born rule from the other assumptions of quantum mechanics, with inconclusive results. . . . The Born rule states that if an observable corresponding to a Hermitian operator A with discrete spectrum is measured in a system with normalized wave function (see bra-ket notation), then the measured result will be one of the eigenvalues λ of A, and the probability of measuring a given eigenvalue λi will equal <ψ|Pi|ψ> where Pi is the projection onto the eigenspace of A corresponding to λi'.' back |
Cantor's paradox - Wikipedia, Cantor's paradox - Wikipedia, the free encyclopedia, 'In set theory, Cantor's paradox is derivable from the theorem that there is no greatest cardinal number, so that the collection of "infinite sizes" is itself infinite. The difficulty is handled in axiomatic set theory by declaring that this collection is not a set but a proper class; in von Neumann–Bernays–Gödel set theory it follows from this and the axiom of limitation of size that this proper class must be in bijection with the class of all sets. Thus, not only are there infinitely many infinities, but this infinity is larger than any of the infinities it enumerates.' back |
Cantor's theorem - Wikipedia, Cantor's theorem - Wikipedia, the free encyclopedia, ' In mathematical set theory, Cantor's theorem is a fundamental result which states that, for any set A , the set of all subsets of A, the power set of A, has a strictly greater cardinality than A itself. For finite sets, Cantor's theorem can be seen to be true by simple enumeration of the number of subsets. Counting the empty set as a subset, a set with n elements has a total of n 2 subsets, and the theorem holds because n2 > n for all non-negative integers. Much more significant is Cantor's discovery of an argument that is applicable to any set, and shows that the theorem holds for infinite sets also.' back |
David Hilbert (1925), On the Infinite, ' We encounter a completely different and quite unique conception of the notion of infinity in the important and fruitful method of ideal elements. The method of ideal elements is used even in elementary plane geometry. The points and straight lines of the plane originally are real, actually existent objects. One of the axioms that hold for them is the axiom of connection: one and only one straight line passes through two points. It follows from this axiom that two straight lines intersect at most at one point. There is no theorem that two straight lines always intersect at some point, however, for the two straight lines might well be parallel. Still we know that by introducing ideal elements, viz., infinitely long lines and points at infinity, we can make the theorem that two straight lines always intersect at one and only one point come out universally true. These ideal "infinite" elements have the advantage of making the system of connection laws as simple and perspicuous as possible. Another example of the use of ideal elements are the familiar complex-imaginary magnitudes of algebra which serve to simplify theorems about the existence and number of the roots of an equation.' back |
Differential geometry - Wikipedia, Differential geometry - Wikipedia,the free encyclopedia, ' Differential geometry is a mathematical discipline that uses the techniques of differential calculus and integral calculus, as well as linear algebra and multilinear algebra, to study problems in geometry. The theory of plane and space curves and of surfaces in the three-dimensional Euclidean space formed the basis for development of differential geometry during the 18th century and the 19th century. Since the late 19th century, differential geometry has grown into a field concerned more generally with the geometric structures on differentiable manifolds.' back |
Dirac equation - Wikipedia, Dirac equation - Wikipedia, the free encyclopedia, 'In particle physics, the Dirac equation is a relativistic wave equation derived by British physicist Paul Dirac in 1928. In its free form, or including electromagnetic interactions, it describes all spin-1⁄2 massive particles such as electrons and quarks, for which parity is a symmetry, and is consistent with both the principles of quantum mechanics and the theory of special relativity, and was the first theory to account fully for special relativity in the context of quantum mechanics. It accounted for the fine details of the hydrogen spectrum in a completely rigorous way.' back |
Dreamtime - Wikipedia, Dreamtime - Wikipedia, the free encyclopedia, ' The Dreaming is used to represent Aboriginal concepts of Everywhen during which the land was inhabited by ancestral figures, often of heroic proportions or with supernatural abilities. These figures were often distinct from gods as they did not control the material world and were not worshipped, but only revered. . . . By the 1990s, Dreaming had acquired its own currency in popular culture, based on idealised or fictionalised conceptions of Australian mythology. Since the 1970s, Dreaming has also returned from academic usage via popular culture and tourism and is now ubiquitous in the English vocabulary of Aboriginal Australians in a kind of "self-fulfilling academic prophecy".' back |
Elementary particle - Wikipedia, Elementary particle - Wikipedia, the free encyclopedia, ' In particle physics, an elementary particle or fundamental particle is a subatomic particle that is not composed of other particles. Particles currently thought to be elementary include the fundamental fermions (quarks, leptons, antiquarks, and antileptons), which generally are "matter particles" and "antimatter particles", as well as the fundamental bosons (gauge bosons and the Higgs boson), which generally are "force particles" that mediate interactions among fermions. A particle containing two or more elementary particles is a composite particle.' back |
Erwin Schrödinger (1926), Quantization is an eigenvalue problem, '§1. In this communication I would like first to show, in the simplest case of the (non-relativistic and unperturbed) hydrogen atom, that the usual prescription for quantisation can be substituted by another requirement in which no word about “integer numbers” occurs anymore. Rather, the integerness emerges in the same natural way as, for example, the integerness of the number of knots of a vibrating string. The new interpretation is generalisable and touches, as I believe, very deeply the true essence of the quantisation prescription.' back |
Evolutionary history of life - Wikipedia, Evolutionary history of life - Wikipedia, the free encyclopedia, 'The evolutionary history of life on Earth traces the processes by which living and fossil organisms have evolved since life appeared on the planet, until the present day. Earth formed about 4.5 Ga (billion years) ago and there is evidence that life appeared as early as 4.1 Ga. The similarities between all present-day organisms indicate the presence of a common ancestor from which all known species have diverged through the process of evolution.' back |
Galileo affair - Wikipedia, Galileo affair - Wikipedia, the free encyclopedia, ' The Galileo affair (Italian: il processo a Galileo Galilei) began around 1610 and culminated with the trial and condemnation of Galileo Galilei by the Roman Catholic Inquisition in 1633. Galileo was prosecuted for his support of heliocentrism, the astronomical model in which the Earth and planets revolve around the Sun at the centre of the Solar System. ' back |
Hebrew Bible - Wikipedia, Hebrew Bible - Wikipedia, the free encyclopedia, ' The Hebrew Bible . . . is a term referring to the books of the Jewish Bible as originally written mostly in Biblical Hebrew with some Biblical Aramaic. The term closely corresponds to contents of the Jewish Tanakh and the Protestant Old Testament (see also Judeo-Christian) but does not include the deuterocanonical portions of the Roman Catholic or the Anagignoskomena portions of the Eastern Orthodox Old Testaments. The term does not imply naming, numbering or ordering of books, which varies (see also Biblical canon).' back |
Hermann Minkowski (1908), Space and Time – lecture given at the 80th Meeting of the Natural Scientists in Cologne on September 21, 1908., ' Gentlemen! The views of space and time which I want to present to you arose from the domain of experimental physics, and therein lies their strength. Their tendency is radical. From now onwards space by itself and time by itself will recede completely to become mere shadows and only a type of union of the two will still stand independently on its own.' back |
Hilbert space - Wikipedia, Hilbert space - Wikipedia, the free encyclopedia, ' In mathematics, Hilbert spaces (named after David Hilbert) allow the methods of linear algebra and calculus to be generalized from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that induces a distance function for which the space is a complete metric space. A Hilbert space is a special case of a Banach space. ' back |
Hilbert's program - Wikipedia, Hilbert's program - Wikipedia, the free encyclopedia, ' In mathematics, Hilbert's program, formulated by German mathematician David Hilbert, was a proposed solution to the foundational crisis of mathematics, when early attempts to clarify the foundations of mathematics were found to suffer from paradoxes and inconsistencies. As a solution, Hilbert proposed to ground all existing theories to a finite, complete set of axioms, and provide a proof that these axioms were consistent. Hilbert proposed that the consistency of more complicated systems, such as real analysis, could be proven in terms of simpler systems. Ultimately, the consistency of all of mathematics could be reduced to basic arithmetic.' back |
Ian Duck and E.C.G. Sudarshan (1998), Toward an understanding of the spin-statistics theorem, 'We respond to a request from Neuenschwander for an elementary proof of the Spin-Statistics Theorem. First . . . Then we discuss an argument suggested by Sudarshan, which proves the theorem with a minimal set of requirements. . . . Motivated by our particular use of Lorentz invariance, if we are permitted to elevate the conclusion of flavour symmetry (which we explain in the text) to the status of a postulate, one could recast the proof without any relativistic assumptions, and this make it applicable even in the nonrelativistic context. . . . Finally, an argument starting with ordinary number-valued (nonmmuting), and with Grassman valued (anticommuting) operators, shows in a natural way that these relativitcally embed into Klein-Gordon spin-0 and Dirac spin-½ fields, respectively. In this way the Spin Statistics theorem is understood at the expense of admitting the existence of the simplest Grassman-valued field.' back |
Isaac Newton (1713), The General Scholium to the Principia Mathematica, 'Published for the first time as an appendix to the 2nd (1713) edition of the Principia, the General Scholium reappeared in the 3rd (1726) edition with some amendments and additions. As well as countering the natural philosophy of Leibniz and the Cartesians, the General Scholium contains an excursion into natural theology and theology proper. In this short text, Newton articulates the design argument (which he fervently believed was furthered by the contents of his Principia), but also includes an oblique argument for a unitarian conception of God and an implicit attack on the doctrine of the Trinity, which Newton saw as a post-biblical corruption. The English translation here is that of Andrew Motte (1729). Italics and orthography as in original.' back |
Isotope - Wikipedia, Isotope - Wikipedia, the free encyclopedia, ' Isotopes are distinct nuclear species (or nuclides) of the same chemical element. They have the same atomic number (number of protons in their nuclei) and position in the periodic table (and hence belong to the same chemical element), but differ in nucleon numbers (mass numbers) due to different numbers of neutrons in their nuclei. While all isotopes of a given element have similar chemical properties, they have different atomic masses and physical properties.' back |
John von Neumann (2014), Mathematical Foundations of Quantum Mechanics, ' Mathematical Foundations of Quantum Mechanics by John von Neumann translated from the German by Robert T. Beyer (New Edition) edited by Nicholas A. Wheeler. Princeton UP Princeton & Oxford. Preface: ' This book is the realization of my long-held intention to someday use the resources of TEX to produce a more easily read version of Robert T. Beyer’s authorized English translation (Princeton University Press, 1955) of John von Neumann’s classic Mathematische Grundlagen der Quantenmechanik (Springer, 1932).'This content downloaded from ������������129.127.145.240 on Sat, 30 May 2020 22:38:31 UTC������������ back |
Katharine Richardson & Xuemei Bal, What are ‘planetary boundaries’ and why should we care?, ' If we keep our activities to a safe level, the sheer exuberance of life and the planet’s own processes can handle it. But in six out of nine vital life support systems, we have blown well past the safe zone. And we’re now in the danger zone, where we – as well as every other species – are now at risk. Planetary boundaries update 2023: Our breach of boundaries is very new In last week’s update, the research team found we had now gone beyond the safe zone into dangerous territory in six of the nine processes. We are still in the green for ozone-depleting chemicals. Ocean-acidification is still, just, in the green, and so is aerosol pollution and dust. But on climate change, deforestation, biodiversity loss, synthetic chemicals such as plastics, freshwater depletion, and nitrogen/phosphorus use, we’re well out of the safer zone. On these six, we’re deep in the red zone.' back |
Kerson Huang (2013), A Critical History of Renormalization, ' The history of renormalization is reviewed with a critical eye,starting with Lorentz's theory of radiation damping, through perturbative QED with Dyson, Gell‐Mann & Low, and others, to Wilson's formulation and Polchinski's functional equation, and applications to "triviality", and dark energy in cosmology. |
Kinematics - Wikipedia, Kinematics - Wikipedia, the free encyclopedia, 'Kinematics (from Greek . . . kinein, to move) is a subfield of physics, developed in classical mechanics, that describes the motion of points, bodies (objects), and systems of bodies (groups of objects) without considering the forces that cause them to move.' back |
Kirchoff's law of thermal radiation - Wikipedia, Kirchoff's law of thermal radiation - Wikipedia, the free encyclopedia, 'Kirchhoff's law states that: For a body of any arbitrary material, emitting and absorbing thermal electromagnetic radiation at every wavelength in thermodynamic equilibrium, the ratio of its emissive power to its dimensionless coefficient of absorption is equal to a universal function only of radiative wavelength and temperature, the perfect black-body emissive power. back |
Klein-Gordon equation - Wikipedia, Klein-Gordon equation - Wikipedia, the free encyclopedia, 'It is the equation of motion of a quantum scalar or pseudoscalar field, a field whose quanta are spinless particles. It cannot be straightforwardly interpreted as a Schrödinger equation for a quantum state, because it is second order in time and because it does not admit a positive definite conserved probability density. Still, with the appropriate interpretation, it does describe the quantum amplitude for finding a point particle in various places, the relativistic wavefunction, but the particle propagates both forwards and backwards in time. Any solution to the Dirac equation is automatically a solution to the Klein–Gordon equation, but the converse is not true.' back |
Last universal common ancestor - Wikipedia, Last universal common ancestor - Wikipedia, the free encyclopedia, ' The last universal common ancestor (LUCA) is the most recent population from which all organisms now living on Earth share common descent—the most recent common ancestor of all current life on Earth. . . . .. While no specific fossil evidence of the LUCA exists, the detailed biochemical similarity of all current life makes it plausible. Its characteristics can be inferred from shared features of modern genomes. These genes describe a complex life form with many co-adapted features, including transcription and translation mechanisms to convert information from DNA to mRNA to proteins. The LUCA probably lived in the high-temperature water of deep sea vents near ocean-floor magma flows around 4 billion years ago.' back |
Matrix mechanics - Wikipedia, Matrix mechanics - Wikipedia, the free encyclopedia, 'Matrix mechanics is a formulation of quantum mechanics created by Werner Heisenberg, Max Born, and Pascual Jordan in 1925. Matrix mechanics was the first conceptually autonomous and logically consistent formulation of quantum mechanics. It extended the Bohr Model by describing how the quantum jumps occur. It did so by interpreting the physical properties of particles as matrices that evolve in time. It is equivalent to the Schrödinger wave formulation of quantum mechanics, and is the basis of Dirac's bra-ket notation for the wave function. back |
Maxwell's equations - Wikipedia, Maxwell's equations - Wikipedia, the free encyclopedia, ' Maxwell's equations are a set of coupled partial differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. The equations provide a mathematical model for electric, optical, and radio technologies, such as power generation, electric motors, wireless communication, lenses, radar etc. They describe how electric and magnetic fields are generated by charges, currents, and changes of the fields.' back |
Meinard Kuhlmann (Stanford Encyclopedia of Philosophy), Quantum Field Theory, ' Quantum Field Theory (QFT) is the mathematical and conceptual framework for contemporary elementary particle physics. In a rather informal sense QFT is the extension of quantum mechanics (QM), dealing with particles, over to fields, i.e. systems with an infinite number of degrees of freedom. (See the entry on quantum mechanics.) In the last few years QFT has become a more widely discussed topic in philosophy of science, with questions ranging from methodology and semantics to ontology. QFT taken seriously in its metaphysical implications seems to give a picture of the world which is at variance with central classical conceptions of particles and fields, and even with some features of QM.' back |
Michael Atiyah (1998), The Dirac equation and geometry,, Available in: M. F. Atiyah: “The Dirac equation and geometry,” pp. 108–124 in A. Pais, M. Jacob, D. I. Olive, and M. F. Atiyah: Paul Dirac: The man and his work. Edited by P. Goddard. Cambridge University Press, 1998. MR 1606723 back |
Michael Faraday - Wikipedia, Michael Faraday - Wikipedia, the free encyclopedia, ' Michael Faraday FRS September 1791 – 25 August 1867) was an English scientist who contributed to the study of electromagnetism and electrochemistry. His main discoveries include the principles underlying electromagnetic induction, diamagnetism and electrolysis. Although Faraday received little formal education, he was one of the most influential scientists in history. It was by his research on the magnetic field around a conductor carrying a direct current that Faraday established the concept of the electromagnetic field in physics. . . . His inventions of electromagnetic rotary devices formed the foundation of electric motor technology, and it was largely due to his efforts that electricity became practical for use in technology.' back |
Minkowski space - Wikipedia, Minkowski space - Wikipedia, the free encyclopedia, ' By 1908 Minkowski realized that the special theory of relativity, introduced by his former student Albert Einstein in 1905 and based on the previous work of Lorentz and Poincaré, could best be understood in a four-dimensional space, since known as the "Minkowski spacetime", in which time and space are not separated entities but intermingled in a four-dimensional space–time, and in which the Lorentz geometry of special relativity can be effectively represented using the invariant interval x2 + y2 + z2 − c2 t2.' back |
Molecular biology - Wikipedia, Molecular biology - Wikipedia, the free encyclopedia, ' Molecular biology . . . is the branch of biology that deals with the molecular basis of biological activity. This field overlaps with other areas of biology and chemistry, particularly genetics and biochemistry. Molecular biology chiefly concerns itself with understanding the interactions between the various systems of a cell, including the interactions between the different types of DNA, RNA and protein biosynthesis as well as learning how these interactions are regulated.' back |
Newton's law of universal gravitation - Wikipedia, Newton's law of universal gravitation - Wikipedia, the free encyclopedia, ' Newton's law of universal gravitation is usually stated as that every particle attracts every other particle in the universe with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between their centers. The publication of the theory has become known as the "first great unification", as it marked the unification of the previously described phenomena of gravity on Earth with known astronomical behaviors.' back |
No cloning theorem - Wikipedia, No cloning theorem - Wikipedia, the free encyclopedia, 'The no cloning theorem is a result of quantum mechanics which forbids the creation of identical copies of an arbitrary unknown quantum state. It was stated by Wootters, Zurek, and Dieks in 1982, and has profound implications in quantum computing and related fields.' back |
Old quantum theory - Wikipedia, Old quantum theory - Wikipedia, the free encyclopedia, ' The old quantum theory is a collection of results from the years 1900–1925 which predate modern quantum mechanics. The theory was never complete or self-consistent, but was rather a set of heuristic corrections to classical mechanics. The theory is now understood as the semi-classical approximation to modern quantum mechanics. The main and final accomplishments of the old quantum theory were the determination of the modern form of the periodic table by Edmund Stoner and the Pauli Exclusion Principle which were both premised on the Arnold Sommerfeld enhancements to the Bohr model of the atom. The main tool of the old quantum theory was the Bohr–Sommerfeld quantization condition, a procedure for selecting out certain states of a classical system as allowed states: the system can then only exist in one of the allowed states and not in any other state.' back |
Planck's Law - Wikipedia, Planck's Law - Wikipedia, the free encyclopedia, ' In physics, Planck's law describes the spectral radiance of electromagnetic radiation at all wavelengths from a black body at temperature T. As a function of frequency ν. back |
Principle of individuation - Wikipedia, Principle of individuation - Wikipedia, the free encyclopedia, ' The principle of individuation is a criterion that individuates or numerically distinguishes the members of the kind for which it is given, that is by which we can supposedly determine, regarding any kind of thing, when we have more than one of them or not. It is also known as a 'criterion of identity' or 'indiscernibility principle'. The history of the consideration of such a principle begins with Aristotle. It was much discussed by the medieval philosopher Duns Scotus (c. 1266–1308) with his "haecceity" and later, during Renaissance, by Francisco Suárez (1548–1617), Bonaventure Baron (1610–1696) and Leibniz (1646–1716). back |
Qubit - Wikipedia, Qubit - Wikipedia, the free encyclopedia, 'A quantum bit, or qubit . . . is a unit of quantum information. That information is described by a state vector in a two-level quantum mechanical system which is formally equivalent to a two-dimensional vector space over the complex numbers. Benjamin Schumacher discovered a way of interpreting quantum states as information. He came up with a way of compressing the information in a state, and storing the information on a smaller number of states. This is now known as Schumacher compression. In the acknowledgments of his paper (Phys. Rev. A 51, 2738), Schumacher states that the term qubit was invented in jest, during his conversations with Bill Wootters.' back |
Renormalization - Wikipedia, Renormalization - Wikipedia, the free encyclopedia, ' Renormalization is a collection of techniques in quantum field theory, the statistical mechanics of fields, and the theory of self-similar geometric structures, that are used to treat infinities arising in calculated quantities by altering values of quantities to compensate for effects of their self-interactions. But even if it were the case that no infinities arose in loop diagrams in quantum field theory, it could be shown that renormalization of mass and fields appearing in the original Lagrangian is necessary.' back |
Rolf Landauer (1999), Information is a Physical Entity, 'Abstract: This paper, associated with a broader conference talk on the fundamental physical limits of information handling, emphasizes the aspects still least appreciated. Information is not an abstract entity but exists only through a physical representation, thus tying it to all the restrictions and possibilities of our real physical universe. The mathematician's vision of an unlimited sequence of totally reliable operations is unlikely to be implementable in this real universe. Speculative remarks about the possible impact of that on the ultimate nature of the laws of physics are included.' back |
Scholasticism - Wikipedia, Scholasticism - Wikipedia, the free encyclopedia, 'Scholasticism is a method of critical thought which dominated teaching by the academics ("scholastics," or "schoolmen") of medieval universities in Europe from about 1100 to 1700, and a program of employing that method in articulating and defending dogma in an increasingly pluralistic context. It originated as an outgrowth of, and a departure from, Christian monastic schools at the earliest European universities. . . . .' back |
Spinor - Wikipedia, Spinor - Wikipedia, the free encyclopedia, 'In geometry and physics, spinors are elements of a (complex) vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight (infinitesimal) rotation. When a sequence of such small rotations is composed (integrated) to form an overall final rotation, however, the resulting spinor transformation depends on which sequence of small rotations was used: unlike vectors and tensors, a spinor transforms to its negative when the space is rotated through a complete turn from 0° to 360°.' back |
Thales - Wikipedia, Thales - Wikipedia, the free encyclopedia, 'Thales of Miletus (Greek: Θαλῆς (ὁ Μιλήσιος), Thalēs; c. 624 – c. 546 BC) was a pre-Socratic Greek philosopher from Miletus in Asia Minor, and one of the Seven Sages of Greece. Many, most notably Aristotle, regard him as the first philosopher in the Greek tradition. Aristotle reported Thales' hypothesis about the nature of matter – that the originating principle of nature was a single material substance: water. |
Theodicy - Wikipedia, Theodicy - Wikipedia, the free encyclopedia, ' In the philosophy of religion, a theodicy (meaning 'vindication of God', from Ancient Greek θεός theos, "god" and δίκη dikē, "justice") is an argument that attempts to resolve the problem of evil that arises when omnipotence, omnibenevolence, and omniscience are all simultaneously ascribed to God. Unlike a defence, which merely tries to demonstrate that the coexistence of God and evil is logically possible, a theodicy additionally provides a framework wherein God's existence is considered plausible. The German philosopher and mathematician Gottfried Leibniz coined the term "theodicy" in 1710 in his work Théodicée, though numerous attempts to resolve the problem of evil had previously been proposed.' back |
Theory of Forms - Wikipedia, Theory of Forms - Wikipedia, the free encyclopedia, 'Plato's theory of Forms or theory of Ideas asserts that non-material abstract (but substantial) forms (or ideas), and not the material world of change known to us through sensation, possess the highest and most fundamental kind of reality. When used in this sense, the word form or idea is often capitalized. Plato speaks of these entities only through the characters (primarily Socrates) of his dialogues who sometimes suggest that these Forms are the only true objects of study that can provide us with genuine knowledge; thus even apart from the very controversial status of the theory, Plato's own views are much in doubt. Plato spoke of Forms in formulating a possible solution to the problem of universals.' back |
Thomas Aquinas, Summa Theologiae, Thomas Aquinas: The medieval theological classic online : 'Because the doctor of Catholic truth ought not only to teach the proficient, but also to instruct beginners (according to the Apostle: As unto little ones in Christ, I gave you milk to drink, not meat -- 1 Cor. 3:1-2), we purpose in this book to treat of whatever belongs to the Christian religion, in such a way as may tend to the instruction of beginners. We have considered that students in this doctrine have not seldom been hampered by what they have found written by other authors, partly on account of the multiplication of useless questions, articles, and arguments, partly also because those things that are needful for them to know are not taught according to the order of the subject matter, but according as the plan of the book might require, or the occasion of the argument offer, partly, too, because frequent repetition brought weariness and confusion to the minds of readers.' back |
Tree of life (biology) - Wikipedia, Tree of life (biology) - Wikipedia, the free encyclopedia, 'The tree of life or universal tree of life is a metaphor used to describe the relationships between organisms, both living and extinct, as described in a famous passage in Charles Darwin's On the Origin of Species (1859).' back |
Unmoved mover - Wikipedia, Unmoved mover - Wikipedia, the free encyclopedia, ' The unmoved mover (Ancient Greek: ὃ οὐ κινούμενον κινεῖ, lit. 'that which moves without being moved' or prime mover (Latin: primum movens) is a concept advanced by Aristotle as a primary cause (or first uncaused cause) or "mover" of all the motion in the universe. As is implicit in the name, the unmoved mover moves other things, but is not itself moved by any prior action. In Book 12 (Greek: Λ) of his Metaphysics, Aristotle describes the unmoved mover as being perfectly beautiful, indivisible, and contemplating only the perfect contemplation: self-contemplation. He equates this concept also with the active intellect. This Aristotelian concept had its roots in cosmological speculations of the earliest Greek pre-Socratic philosophers and became highly influential and widely drawn upon in medieval philosophy and theology. St. Thomas Aquinas, for example, elaborated on the unmoved mover in the Quinque viae. ' back |
Wave-particle duality - Wikipedia, Wave-particle duality - Wikipedia, the free encyclopedia, ' Wave–particle duality is the concept in quantum mechanics that every particle or quantum entity may be described as either a particle or a wave. It expresses the inability of the classical concepts "particle" or "wave" to fully describe the behaviour of quantum-scale objects. As Albert Einstein wrote: It seems as though we must use sometimes the one theory and sometimes the other, while at times we may use either. We are faced with a new kind of difficulty. We have two contradictory pictures of reality; separately neither of them fully explains the phenomena of light, but together they do. Through the work of Max Planck, Albert Einstein, Louis de Broglie, Arthur Compton, Niels Bohr, Erwin Schrödinger and many others, current scientific theory holds that all particles exhibit a wave nature and vice versa. back |
Whitehead and Russell (1910), Principia Mathematica, Jacket: 'Principia Mathematica was first published in 1910-1913; this is the fifth impression of the second edition of 1925-7. The Principia has long been recognized as one of the intellectual landmarks of the century. It was the first book to show clearly the close relationship between mathematics and formal logic. Starting with a minimal number of axioms, Whitehead and Russell display the structure of both kinds of thought. No other book has had such an influence on the subsequent history of mathematical philosophy .' back |
William Bialek & Allan Schweitzer (1985), Quantum Noise and the Threshold of Hearing, ' We argue that the sensitivity of the ear reaches a limit imposed by the uncertainty principle. This is possible only if the receptor holds the detector elements in a special nonequilibirium state which has the same noise characteristics as a ground (T = 0 K) state. To accomplish this "active cooling" the molecular dynamics of the system must maintain quantum mechanical coherence over the time scale of the measurement.' back |